본 블로그 포스트에서 사용된 표, 이미지 및 기타 관련 자료는 해당 논문에서 발췌한 것입니다. 이 자료들은 논문의 내용을 요약하고 이해를 돕기 위한 참고용으로 제공됩니다. 또한, 해석 과정에서 일부 오류가 있을 수 있으니 원 논문을 참고하여 확인하시기 바랍니다.
Abstract
이 논문은 비지도 학습 상황에서 유용한 표현(Representation)을 학습하는 문제를 해결하고자, 간단하면서도 강력한 생성 모델인 VQ-VAE(Vector Quantised Variational AutoEncoder)를 제안한다. VQ-VAE는 기존 VAE 와는 다음 두 가지 주요 차이를 가진다.
㉮ Encoder 출력이 연속값이 아닌 이산(discrete) 코드로 구성됨
㉯ Prior가 고정(static)된 분포가 아닌 학습 가능한 분포로 설정됨
또한, 벡터 양자화(Vector Quantization, VQ) 기법을 도입하여 강력한 autoregressive 디코더 사용 시 발생하는 posterior collapse 문제를 효과적으로 해결한다. 학습된 이산 표현은 이미지, 비디오, 음성의 고품질 생성뿐 아니라, 화자 변환 및 음소 수준 의 비지도 학습에도 활용 가능함을 통해 그 표현의 유용성을 입증한다.
1. Introduction
최근 이미지, 오디오, 비디오 생성 모델에서 인상적인 성과가 있었지만, few shot learning, domain adaptation, reinforcement learning 과 같은 어려운 과제에서는 여전히 비지도 방식으로 학습된 범용 표현의 활용이 널리 확산되지 못하고 있다. 비지도 모델 학습에서 최대 우도와 재구성 오차가 흔히 활용되지만, 이들의 효과는 활용 분야에 따라 다르다. 본 논문에서는 최대우도를 최적화하면서도 데이터의 중요한 특징을 잠재 공간에 보존하는 모델을 목표로 한다. 기존 연구는 강력한 디코더만으로도 좋은 생성 모델을 만들 수 있다고 제안하지만, 우리는 다양한 영역에서 유용한 이산 잠재변수 학습의 필요성을 주장한다. 기존 연구들은 주로 연속적인 특징 기반의 표현 학습에 집중해왔으나, 본 논문은 언어나 음성 등 다양한 모달리티에 자연스럽게 적용할 수 있는 이산 표현 학습에 초점을 맞춘다. 이산 표현은 복잡한 추론, 계획, 예측 학습에 적합하며, 이를 모델링하기 위한 강력한 자기회귀 모델들도 개발되어 왔다. 본 논문은 벡터 양자화(VQ)를 활용해 이산 잠재 표현을 도입한 새로운 VAE 계열 생성모델(VQ-VAE)을 제안한다. VQ-VAE는 학습이 간단하고 사후 붕괴(posterior collapse) 문제를 효과적으로 방지하며, 기존 연속 잠재변수 VAE와 유사한 성능을 달성하는 최초의 이산 잠재 VAE 모델이다. VQ-VAE는 잠재 공간을 효과적으로 활용해 이미지의 객체, 음성의 음소 등 여러 차원에 걸친 데이터의 중요한 특징을 효율적으로 모델링할 수 있으며, 이는 국소적인 잡음이나 미세한 세부사항에 모델의 용량을 소모하는 기존 방식과 대조된다. 최근, 일단 VQ-VAE로 좋은 이상 잠재 구조 모달리티가 발견된다면, 우리는 이러한 이산형 임의 변수를 넘어 강력한 사전지식을 학습하여, 흥미로운 샘플과 유용한 어플리케이션을 생성한다. 예를 들어, 연설 학습시 우리는 지도 또는 사전 지식없이 언어의 잠재구조를 발견한다. 게다가, 우리는 번역을 위해 출력에 디코더를 장착할 수 있다. VQ-VAE가 모달리티의 이산 잠재 구조를 잘 학습하면, 이 위에 강력한 사전 분포를 학습시켜 다양한 흥미로운 샘플과 유용한 응용이 가능하다. 예를 들어, 음성에 적용하면 무감독으로 언어의 잠재 구조를 발견할 수 있고, 화자 정보를 추가하면 음성의 내용은 그대로 두고 화자만 변환하는 것도 할 수 있다. 또한 강화학습 환경의 장기 구조 학습에서도 유의미한 성과를 보였다.
본 논문의 주요 기여는 다음과 같다.
㉮ VQ-VAE 모델 제안: 간단한 구조이며, 이산 잠재 변수를 사용하고, posterior collaspe나 gradient 분산 문제 없이 안정적으로 학습 가능하다.
㉯ 성능 입증: 이산 잠재 모델인 VQ-VAE 는 로그우도(log-likelihood) 측면에서 연속 잠재 모델과 동등한 성능을 달성함
㉰ 강력한 사전 분포 결합 시 우수한 생성 품질: 음성 및 영상 생성과 같은 다양한 응용 분야에서 일관성 있고 고품질의 샘플을 생성한다.
㉱ 비지도 언어 및 화자 학습: 원시 음성 데이터를 통해 지도 없이 언어 구조를 학습하고, 비지도 화자 변환 응용이 가능함을 실증한다.
2. Related Work
본 논문에서는 이산 변수를 사용하는 변분 오토인코더의 새로운 학습 방법을 제안한다. 기존 딥러닝에서는 대부분 연속 변수 기반의 잠재 표현이 사용되어 왔으며, 이는 이산 변수 학습이 어렵다는 점을 시사한다. 이산 VAE 학습을 위한 다양한 대안들이 존재하는데, 예를 들어 NVIL은 단일 샘플 기반 목적함수를 사용하고 분산 감소 기법을 활용하여 학습을 가속화하며, VIMCO는 다중 샘플 기반 목적함수를 최적화함으로써 추론 네트워크로부터 여러 샘플을 사용해 수렴 속도를 높인다. 그러나, 위의 방법들은 가우시안 재매개화 기법을 사용할 수 있는 연속 잠재 변수 VAE의 성능 격차를 해소하지 못한다. 또한 대부분의 기법들은 MNIST와 같은 소규모 데이터셋과 낮은 차원의 잠재 공간에서만 평가되었다. 반면 본 논문에서는 CIFAR-10, ImageNet, DeepMind Lab 등의 복잡한 이미지 데이터셋과 원시 음성 데이터셋(VCTK)을 사용하여 평가를 수행하였다. 본 논문은 VAE 디코더나 사전 분포에 자기회귀 분포를 사용하는 기존 연구를 확장한 것이다. 이전에는 LSTM 디코더를 활용한 언어 모델링, 팽창 합성곱( decoder with dilated convolution), PixelCNN 기반 디코더 등이 이에 해당한다. 또한 본 논문은 신경망 기반 이미지 압축 연구와도 관련이 있다. 일부 연구는 "스칼라 양자화(scalar quantization)"나 "벡터 양자화(vector quantization)"을 이용해 인코더 출력을 압축한 뒤 부호화하는 방법을 제안했다. 이들 중 일부는 벡터 양자화를 연속적으로 이완한 후 훈련 중 점차 경직(hard)된 군집화를 유도하는 soft-to-hard relaxtion 방식을 사용했으며, 먼저 오토인코더를 학습한 뒤 양자화를 적용하고, 전체 네트워크를 미세 조정하는 방식을 택했다. 그러나 본 연구에서는 이 방식으로 학습을 처음부터 진행할 경우, 디코더가 연속 표현을 역변환해 실제 양자화가 이루어지지 않아 학습이 실패함을 발견하였다.
※Soft to hard relaxation 이란?
부드러운 선택에서 점점 하나만 고르는 이산 선택으로 전환하는 학습 기법이다. 딱 하나만 고르는 이산 선택(hard decision)은 역전파가 불가능하다. 하지만 신경망 학습은 연속적 변화(미분 가능성)을 필요로 한다. 그래서 처음엔 Soft 단계로 여러 후보에 확률적으로 가중치를 분배하고 학습이 진행될수록 하나의 확실한 선택으로 바꾸기 위해 분포가 한곳으로 몰리게 가중치를 분배한다.
Soft-to-Hard Relaxation은 이산적인 연산(예: 양자화, 이산 선택, 샘플링 등)이 포함된 딥러닝 모델에서 이를 미분 가능한 형태로 근사함으로써, 전체 신경망을 종단간(end-to-end)으로 학습할 수 있도록 해주는 기법이다. 이산 연산은 본질적으로 미분이 불가능하기 때문에, 역전파를 기반으로 한 신경망 학습에서 직접적으로 포함시키기 어렵다. 따라서 이를 해결하기 위해 soft-to-hard relaxation 방식이 고안되었다.
이 방식은 학습 초기에는 부드러운 연산(soft operation)으로 시작한다. 예를 들어, hard assignment 대신 softmax 기반의 soft assignment를 사용하여 여러 선택지에 확률적으로 가중치를 분배한다. 이렇게 하면 각 선택에 대한 확률이 연속적으로 표현되므로, 미분이 가능하고 gradient 계산이 원활해진다. 이후 학습이 진행됨에 따라 softmax의 temperature를 점차 낮추거나 기타 scheduling 방법을 사용하여 soft한 분포를 점점 sharpen 시킨다. 그 결과, soft assignment는 점점 하나의 선택지로 수렴하게 되고, 최종적으로는 실제 이산 선택(hard decision)과 동일한 형태로 전환된다.
이 방식의 가장 큰 장점은 학습 과정에서의 유연한 gradient 흐름과 학습 종료 후의 정확한 이산 결정을 동시에 달성할 수 있다는 점이다. 특히 train과 test 시에 soft/hard 간의 불일치로 인해 성능이 저하되는 문제도 줄일 수 있다. 이러한 이유로 soft-to-hard relaxation은 VQ-VAE, Gumbel-Softmax, 이미지 압축, 이산 잠재 변수 학습 등 다양한 분야에서 활발히 사용되고 있다.
단점으로는 annealing 스케줄이나 temperature 조정과 같은 하이퍼파라미터의 민감성이 있으며, 잘못된 조정은 hard 단계에서의 성능 저하로 이어질 수 있다. 그럼에도 불구하고, 이산 구조를 학습하는 데 있어서 soft-to-hard relaxation은 중요한 역할을 하며, 신경망의 학습 가능성과 표현력을 동시에 향상시키는 유용한 방법으로 평가받고 있다.
※ 벡터 양자화란
복잡한 숫자들을 비슷한 것끼리 묶어서, 대표 숫자 하나로 대신 표현하는 방법이다. 예를 들어, 여러 색깔이 섞인 그림을 보고 있다고 가정하자. 그런데 저장 공간이 부족해서 색깔을 전부 저장할 수 없다면, 보통 비슷한 색끼리 묶어서, 그 중 대표 색 하나만 골라서 저장을 할 것이다. 이것이 바로 벡터 양자화이다.
딥러닝 모델은 이미지나 음성 등에서 복잡한 특징 벡터(feature vector)를 뽑는다. 이 벡터는 숫자 여러 개로 이루어진 일종의 좌표다. 이것을 그대로 사용하면 계산량도 많고 저장도 복잡하여, 다음과 같이 처리한다.
㉮ 사전에 여러 대표 벡터를 만들어 놓는다.
㉯ 입력 벡터가 들어오면, 그 중 가장 가까운 대표 벡터 하나로 바꿔서 사용한다.
이렇게 하면, 입력 데이터는 오직 '어떤 대표 벡터에 속하는가"만으로 표현되므로, 훨씬 간단하고 효율적으로 처리할 수 있다.
벡터 양자화의 주요 종류
1. 일반 벡터 양자화 (Standard VQ)
1) 가장 기본적인 형태로, 각 입력 벡터 $x$를 유클리드 거리 기준으로 가장 가까운 코드워드 $e_k$로 대체
2) 학습은 k-means 또는 SGD 기반으로 이루어짐
2. 적응형 벡터 양자화 (Adaptive VQ)
1) 데이터 분포의 변화나 불균형에 따라 코드북이 적응적으로 업데이트됨
2) EM 알고리즘 또는 가중치 기반 업데이트를 활용
3. 잔차 양자화 (Residual VQ, RVQ)
1) 첫 번째 양자화 후 남은 오차(residual)를 다시 양자화하여 계층적으로 표현
2) $x \approx e_{k_1} + r_1, \quad r_1 \approx e_{k_2} + r_2, \ldots$ 형태
3) 고정된 코드북 크기로 높은 표현력을 달성 가능
4. 제품 양자화 (Product Quantization, PQ)
1) 고차원 벡터를 $M$개의 저차원 서브벡터로 분할하여 각 부분별로 독립적인 코드북을 학습
2) 전체 코드북 수가 $K^M$으로 지수적으로 증가하므로 \\고차원 근사 검색(ANN)\\에 자주 활용
3) Facebook FAISS 라이브러리에서 대표적으로 사용
5. 계층적 벡터 양자화 (Hierarchical VQ)
1) VQ 단계를 트리 구조로 구성하여 coarse-to-fine 방식으로 양자화 수행
2) 검색 및 생성 시 다중 단계에서 점진적 refinement 가능
6. 학습 기반 벡터 양자화 (e.g., VQ-VAE)
1) 코드북을 딥러닝 모델과 함께 end-to-end로 학습
2) VQ-VAE에서는 straight-through estimator와 commitment loss를 사용하여 encoder, decoder, codebook을 공동 최적화함
딥러닝에서의 활용
1. VQ-VAE: 이산 잠재 표현 학습, posterior collapse 방지
2. Neural Compression: 양자화된 feature map의 효율적 인코딩
3. Gumbel-Softmax와의 비교: soft differentiable 방식과 달리 실제 hard assignment 사용
4, Unsupervised Discrete Representation Learning: 음성, 언어, 영상 등에서 구조적 표현 학습 가능
장단점
| 장점 | 설명 |
| 압축 효과 | 이산 인덱스로 표현하므로 메모리 절약 가능 |
| 계산 효율성 | NN 검색 및 코드북 참조 방식으로 연산 단순화 |
| 표현력 향상 | 계층적/잔차 구조와 결합하면 매우 높은 압축률과 재구성 정확도 가능 |
| 딥러닝 통합 가능 | end-to-end 학습을 통한 표현 최적화 |
| 단점 | 설명 |
| 양자화 손실 | 원본 벡터와 대표 벡터 간 거리로 인한 재구성 오류 발생 |
| 코드북 붕괴 | 일부 코드워드만 사용되어 다양성 상실 가능 (특히 학습 초기) |
| 비미분성 문제 | argmin 연산이 gradient 전파 불가 → straight-through estimator 또는 soft-to-hard relaxation 필요 |
결론
벡터 양자화는 고차원 데이터를 이산적인 코드로 변환하여 압축성과 계산 효율을 극대화하는 기술이다. 전통적인 압축 기법에서 출발하여, 최근에는 VQ-VAE, Residual VQ, Product Quantization 등의 발전을 통해 딥러닝과 결합되어 이산 표현 학습(discrete representation learning)의 핵심 수단으로 자리잡았다. 각각의 양자화 방식은 용도(압축, 검색, 생성 등)와 데이터 특성에 따라 선택적으로 활용되며, 향후에는 self-supervised learning이나 multimodal representation 분야로의 확장이 기대된다.
3. VQ-VAE
이 문단에서는 기존 VAE(Variational Autoencoder) 구조와 본 논문에서 제안하는 VQ-VAE의 차이점을 설명하고 있다. 기존 VAE는 입력 데이터 $x$로부터 잠재 변수 $z$의 사후분포 $q(z \mid x)$, 사전분포 $p(z)$, 그리고 복원 분포 $p(x \mid z)$를 구성하며, 일반적으로 정규분포(gaussian)을 가정하고 가우시안 재매개화 기법을 사용한다. 확장된 VAE에서는 자기회귀 모델, 정규화 흐름(normalizing flows), 역자기회귀 posterior 등이 도입되었다. 반면, 본 논문에서는 이산 잠재 변수(discrete latent variables)와 벡터 양자화(VQ)에 기반한 새로운 학습 방식을 도입한 VQ-VAE를 제안한다. VQ-VAE에서는 posterior와 prior가 모두 범주형 분포(categorical distribution)로 정의되며, 샘플은 임베딩 테이블의 인덱스로 작용하고, 선택된 임베딩 벡터는 디코더의 입력으로 사용된다.
3.1 Discrete Latent variables
우리는 잠재 임베딩 공간 $e \in \mathbb{R}^{K \times D}$를 정의한다. 여기서 $K$는 이산 잠재 공간의 크기(즉, $K$-분류 범주형 분포를 의미)이며, $D$는 각 잠재 임베딩 벡터 $e_i$의 차원이다. 즉, 총 $K$개의 임베딩 벡터 $e_i \in \mathbb{R}^D$, $i = 1, 2, ..., K$가 존재한다.
모델은 입력 $x$를 받아 이를 인코더에 통과시켜 출력 $z_e(x)$를 생성한다. 그 후 이산 잠재 변수 $z$는 공통 임베딩 공간 $e$ 내에서 가장 가까운 임베딩 벡터를 찾는 최근접 탐색(nearest neighbor lookup)을 통해 결정된다. 이 과정은 식 (1)에 명시되어 있다. 디코더의 입력은 해당 인덱스에 대응하는 임베딩 벡터 $e_k$로, 식 (2)에 정의된다.
이러한 순전파 구조는 일반적인 오토인코더와 유사하지만, 잠재 벡터가 $K$개의 임베딩 중 하나로 매핑되는 비선형적(discrete non-linearity) 처리 방식을 갖는다. 모델의 전체 파라미터는 인코더, 디코더, 그리고 임베딩 공간 $e$의 파라미터로 구성된다.
단순화를 위해 본 절에서는 단일 이산 잠재 변수 $z$를 사용해 설명하지만, 실제 응용에 있어 음성, 이미지, 영상에 대해서는 각각 1차원, 2차원, 3차원의 잠재 표현 공간(latent feature space)을 사용한다.
사후 확률 분포 $q(z|x)$는 범주형 분포로 정의되며, one-hot 형식으로 다음과 같이 표현된다:
$$
q(z = k | x) =
\begin{cases}
1 & \text{if } k = \arg\min_j \| z_e(x) - e_j \|_2 \\
0 & \text{otherwise}
\end{cases}
\tag{1}
$$
※ 수식 1의 이해
1. $z_e(x)$는 인코더의 출력 벡터다.
예: $z_e(x) \in \mathbb{R}^D$
즉, 연속적인 실수 벡터다. (예: $[0.2, -1.1, 3.0, \ldots]$)
2. $e_j$는 코드북의 $j$-번째 임베딩 벡터다.
총 $K$개의 벡터가 존재하며, 각각 $\mathbb{R}^D$ 차원이다.
3. $\| z_e(x) - e_j \|_2$는 유클리드 거리다.
즉, $z_e(x)$와 $e_j$ 사이의 거리 (실수값)
4. $\arg\min_j$는 "가장 가까운 $e_j$의 인덱스 $k$"를 선택한다.
즉, 가장 가까운 대표 벡터를 선택하는 것이다..
5. q(z = k | x)는 one-hot 벡터로 표현된다.
전체 $K$개의 클래스 중, 가장 가까운 $e_k$에 해당하는 한 개의 위치만 1이고 나머지는 0인 one-hot 벡터를 의미한다.
예: $K = 5$, 가장 가까운 벡터가 $e_2$면 → $q(z|x) = [0, 1, 0, 0, 0]$
예: $K = 8$, 가장 가까운 벡터가 $e_5$면 → $q(z|x) = [0, 0, 0, 0, 1, 0, 0, 0]$
즉, $\| z_e(x) - e_j \|$의 거리들 중 가장 작은 인덱스를 선택해서 그 인덱스만 1로 표시한 one-hot 벡터를 만드는 구조인 것이다.
여기서 $z_e(x)$는 인코더 네트워크의 출력이다. 우리는 이 모델을 변분 오토인코더(VAE)의 구조로 간주할 수 있으며, $\log p(x)$를 ELBO (Evidence Lower Bound)로 하한 설정할 수 있다. 본 논문에서는 $q(z = k | x)$를 결정적(deterministic) 분포로 간주하며, $z$에 대해 단순한 균일 사전분포(uniform prior)를 설정함으로써, Kullback-Leibler 발산(KL divergence)은 상수값인 $\log K$로 고정된다.
※ Kullback-Leibler 발산(KL divergence)은 상수값인 $\log K$로 고정되는 이유
1. 기본 식
변분 오토인코더(VAE)의 증거 하한(ELBO)은 다음과 같이 표현된다:
$$\log p(x) \geq \mathbb{E}_{q(z|x)} [\log p(x|z)] - D_{\text{KL}}(q(z|x) \| p(z))$$
2. VQ-VAE에서는?
(1) Posterior $q(z|x)$:
one-hot 결정적(discrete and deterministic) 선택
즉, 확률분포가 아니라 특정 $k$에 대해 1, 나머지는 0 → 확률 분포로서 엔트로피가 0
(2) Prior $p(z)$:
학습 중에는 uniform distribution으로 고정됨
즉, $p(z) = \frac{1}{K}$
(3) KL 항 계산
$$D_{\text{KL}}(q(z|x) \| p(z)) = \sum_{k=1}^{K} q(z = k|x) \log \frac{q(z = k|x)}{p(z = k)} = \log K$$
$q(z|x)$는 one-hot이므로 선택된 $k$만 고려 → $\log \frac{1}{1/K} = \log K$. 따라서 KL 항은 항상 상수임
인코더의 출력 $z_e(x)$는 양자화 병목(discretisation bottleneck)을 통과한 후, 임베딩 $e$ 내 가장 가까운 요소로 매핑되며, 이는 다음과 같은 식으로 정의된다:
$$
z_q(x) = e_k, \quad \text{where } k = \arg\min_j \| z_e(x) - e_j \|_2
\tag{2}
$$
이로써, 입력은 이산 잠재 공간 내에서 최적의 임베딩 벡터로 매핑되어 디코더의 입력으로 사용된다.
[질문]
입력이 $z_e(x) = [0.2, 0.3, 0.1, 0.15, ..., 0.5]$와 같은 벡터이고, embedding space에 $e_1, e_2, ..., e_K$ 벡터들이 있다면,
각 $e_j$와 유클리드 거리를 계산해서 가장 가까운 $e_k$를 선택한 후 $q(z|x)$는 one-hot 벡터가 되고 디코더 입력 $z_q(x)$는 선택된 $e_k$가 되는 게 맞나요?
[답]
네, 맞습니다.
1. 입력 $z_e(x)$는 인코더의 출력으로, 실수 벡터입니다.
2. 이 벡터는 임베딩 테이블 $e_1, ..., e_K$ 내의 모든 벡터들과 유클리드 거리를 계산합니다.
3. 그 중 가장 가까운 벡터 $e_k$를 선택합니다:
$$
k = \arg\min_j \| z_e(x) - e_j \|_2
$$
4. Posterior 분포 $q(z|x)$는 이 선택 결과를 반영한 one-hot 벡터가 됩니다:
$$
q(z|x) = [0, ..., 1, ..., 0] \quad (\text{k번째만 1})
$$
5. 디코더 입력 $z_q(x)$는 해당 임베딩 벡터 그 자체입니다:
$$
z_q(x) = e_k
$$
따라서 요약하면,
인코더 출력 $z_e(x)$ → 가장 가까운 $e_k$ 선택 →
$q(z|x)$는 one-hot → $z_q(x)$는 $e_k$ 로 처리되는 것이 맞습니다.
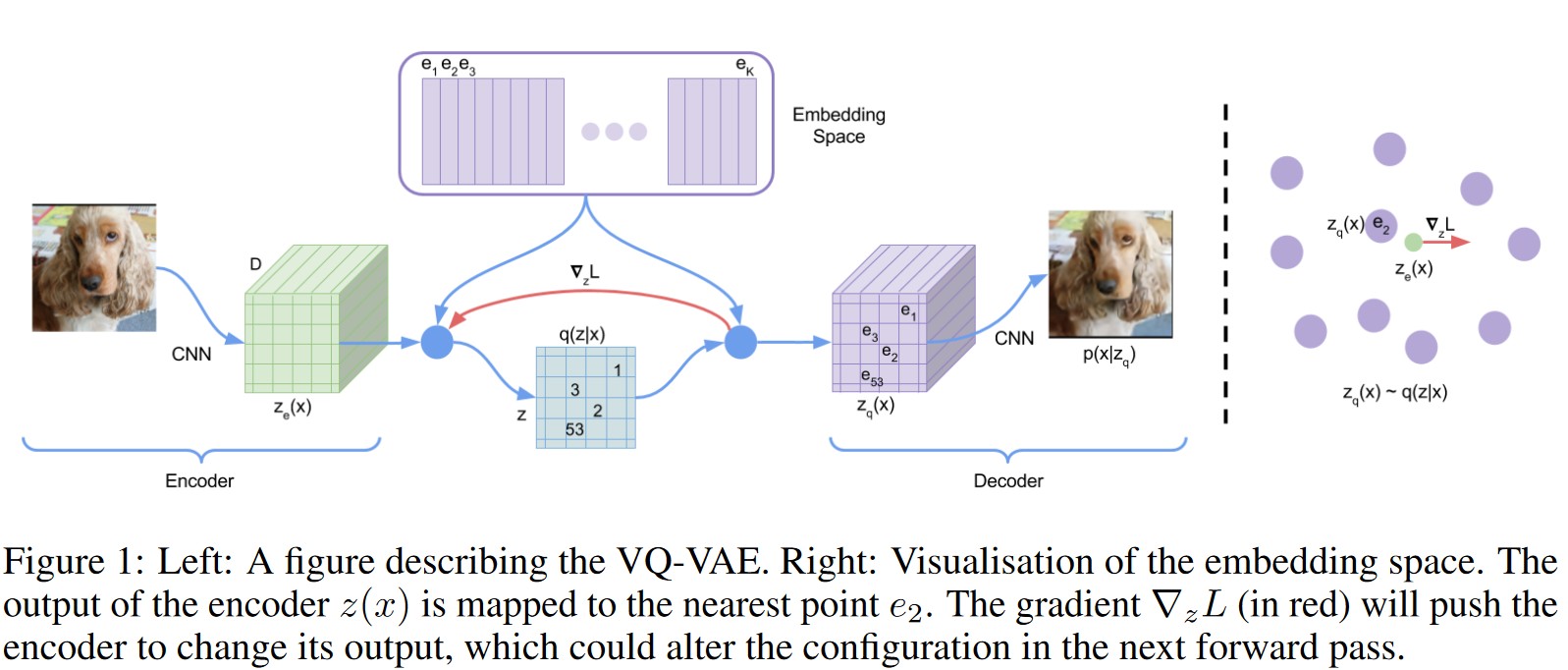
3.2 Learning
식 (2)에 대해서는 정의된 명시적인 gradient가 존재하지 않지만, 우리는 straight-through estimator(*) 방식과 유사하게 근사하여, 디코더 입력인 $z_q(x)$에서 인코더 출력 $z_e(x)$로 gradient를 그대로 복사한다. 양자화 연산에 대해 부분 도함수(subgradient)를 사용하는 방식도 고려할 수 있지만, 본 논문에서는 단순한 이 방식이 초기 실험에서 잘 작동하였다. 순전파(forward computation) 과정에서는 가장 가까운 임베딩 $z_q(x)$(식 2에 정의됨)이 디코더로 전달되며, 역전파(backward pass)에서는 재구성 손실에 대한 gradient $\nabla_z \mathcal{L}$가 변형 없이 인코더로 전달된다. 인코더의 출력과 디코더의 입력이 동일한 차원 $D$의 공간을 보유하기 때문에, 이러한 gradient는 인코더가 재구성 오차를 줄이기 위해 출력을 어떻게 조정해야 할지를 알려주는 유용한 정보를 포함하게 된다.
※Straight-Through Estimator 란 무엇인가?
Straight-Through Estimator(STE)는 딥러닝 모델 내에 포함된 미분 불가능한 연산—예를 들어 이산화(discretization), 반올림(rounding), 양자화(quantization), 부호 함수(sign), argmax 등—에 대해, 학습 과정의 역전파 단계에서 gradient를 정의할 수 없거나 gradient가 0이 되는 문제를 해결하기 위한 근사적 기법이다. 딥러닝에서 학습은 역전파(backpropagation)를 통해 이루어지는데, 이 과정에서는 각 연산의 도함수(gradient)가 존재해야 한다. 하지만 앞서 언급한 이산 연산들은 거의 모든 구간에서 미분이 불가능하거나 도함수가 0이기 때문에, 역전파 시 gradient가 사라지는 현상(vanishing gradient)이 발생하고, 이로 인해 파라미터 업데이트가 불가능해지는 문제가 생긴다.이를 해결하기 위해 STE는 다음과 같은 방식으로 작동한다. 순전파(forward) 시에는 실제로 미분 불가능한 연산을 그대로 사용하여 이산화 또는 양자화된 출력을 얻는다. 하지만 역전파 단계에서는 해당 연산의 도함수를 실제로 계산하지 않고, 마치 항등 함수(identity function)의 도함수를 사용하는 것처럼 처리한다. 다시 말해, 실제 함수는 미분 불가능하지만, 역전파 시에는 gradient를 그대로 통과(straight-through)시키는 방식이다. 예를 들어, forward에서는 $y = \text{sign}(x)$와 같은 비연속 연산을 사용하지만, backward에서는 $\frac{dy}{dx} = 1$로 간주하여 gradient를 복사하듯 넘긴다. 이러한 방식은 gradient를 신경망의 상위 계층에서 하위 계층으로 흘려보낼 수 있도록 하여 학습을 가능하게 만든다. STE는 특히 이산 표현이 필요한 여러 분야에서 널리 사용되며, 대표적인 활용 사례로는 VQ-VAE(Vector Quantized Variational AutoEncoder), Gumbel-Softmax, 이진화된 신경망(Binarized Neural Networks) 및 양자화된 신경망(Quantized Neural Networks) 등이 있다. 핵심은, STE는 역전파 단계에서 실제 미분 가능한 수학적 정의를 따르지 않고, 임의로 정의한 gradient 경로(보통 항등 함수의 도함수처럼)를 통해 연산의 학습 가능성을 유지시킨다는 점이다. 이처럼 STE는 이산 연산이 포함된 신경망에서 학습 가능성을 확보하기 위한 중요한 근사 기법으로 자리 잡고 있다.
그림1(오른쪽)에서 볼 수 있듯이, 이 gradient는 인코더 출력을 다음 순전파에서 다르게 양자화(discrete)되도록 유도할 수 있다. 왜냐하면 식(1)의 최근접 선택 결과가 변경될 수 있기 때문이다. 다음 순전파(forward pass)에서 양자화 결과가 달라지는 이유는, 양자화 연산 자체 때문이 아니다. 보다 정확하게는, 이전 학습 단계의 역전파(backward pass) 과정에서 인코더의 출력인 $z_e(x)$가 gradient에 의해 업데이트되었기 때문에, 이후의 순전파에서 달라진 $z_e(x)$가 이전과는 다른 코드북 벡터 $e_k$에 더 가까워지게 되고, 그 결과 양자화 결과가 달라질 수 있는 것이다. 이러한 변화는 다음과 같은 과정을 통해 발생한다. 먼저, 순전파 단계에서 인코더는 입력 $x$를 받아 $z_e(x)$라는 연속 벡터를 출력하고, 이는 가장 가까운 코드북 벡터 $e_k$로 양자화된다. 이때 선택된 $e_k$는 디코더의 입력 $z_q(x)$로 전달된다. 다음으로, 역전파 단계에서는 Straight-Through Estimator(STE) 기법을 사용하여, 디코더 입력 $z_q(x)$에 대한 gradient를 그대로 인코더 출력 $z_e(x)$에 전달한다. 즉, gradient를 마치 항등 함수처럼 통과시키는 것이다. 이 gradient에 의해 인코더는 다음 학습 반복에서 $z_e(x)$를 약간 다른 방향으로 출력하게 되며, 그 결과 다음 순전파 시점에서는 $z_e(x)$가 이전보다 다른 코드북 벡터에 더 가까워질 수 있다. 이로 인해 양자화된 인덱스 $k$가 바뀌고, 선택되는 임베딩 벡터도 달라진다. 요약하면, VQ-VAE에서 양자화 결과가 순전파마다 바뀌는 근본적인 이유는, 양자화 연산 자체의 불안정성 때문이 아니라, 이전 역전파 과정에서 인코더 출력이 바뀌었기 때문이며, 이로 인해 양자화된 결과 역시 달라질 수 있는 것이다.
식(3)은 전체 손실 함수를 나타내며, 이는 VQ-VAE의 서로 다른 구성 요소를 학습하기 위해 세 가지 항으로 구성된다.
㉮ 첫 번째 항은 재구성 손실(또는 데이터 항)로, 디코더와 인코더를 학습시키는 역할을 하며, 위에서 설명한 gradient 추정 방법을 통해 이루어진다.
㉯ 하지만, $z_(e)$에서 $z_q(x)$로의 매핑은 straight-through 방식으로 gradient를 전달하므로, 임베딩 벡터 $e_i$는 재구성 손실 $\log p(x \mid z_q(x))$로부터 직접적인 gradient를 받지 못한다.
[질문]
임베딩 벡터 $e_i$는 재구성 손실 $\log p(x \mid z_q(x))$로부터 직접적인 gradient를 받지 못한다는 말은, backpropagation 계산 시 gradient가 전달되지 않는다는 뜻인가요?
[답]
네, 맞습니다.
이는 \\backpropagation 계산 시 임베딩 벡터 $e_i$\\로 gradient가 흐르지 않는다는 의미입니다.
그 이유는 \\양자화 과정(embedding lookup)\\이 미분 불가능한 비연속적인 선택 연산이기 때문입니다.
자세한 설명
1. 디코더 입력 $z_q(x)$는 어떻게 만들어지는가?
$$
z_q(x) = e_k, \quad \text{where } k = \arg\min_j \| z_e(x) - e_j \|_2
$$
즉, $z_e(x)$와 가장 가까운 $e_k$를 선택해서 그 자체를 디코더에 넘깁니다.
이때, $k$를 선택하는 연산은 argmin이므로, gradient를 계산할 수 없습니다.
2. 그래서 backpropagation은 어떻게 되는가?
Straight-Through Estimator(STE)는 gradient를 인코더 출력 $z_e(x)$로는 강제로 복사해서 넘기지만,
선택된 임베딩 벡터 $e_k$에는 gradient가 직접적으로 전달되지 않습니다.
즉, 재구성 손실 $\log p(x \mid z_q(x))$은 디코더 파라미터와 $z_e(x)$만 업데이트하고,
$e_k$는 이 경로를 통해 gradient를 받지 못합니다.
3. 그래서 VQ-VAE는 어떻게 임베딩 $e_i$를 학습시키는가?
이를 해결하기 위해, VQ-VAE는 재구성 손실과는 별도로
다음과 같은 벡터 양자화 손실(VQ loss)을 정의합니다:
$$
\| \text{sg}[z_e(x)] - e \|_2^2
$$
여기서 `sg`는 stop-gradient 연산자로,
이 손실은 오직 $e_i$만 업데이트하도록 설계된 loss입니다.
요약 문장
> 임베딩 벡터 $e_i$는 양자화 선택 연산이 미분 불가능하기 때문에,
> 재구성 손실로부터의 backpropagation 경로를 통해 직접적으로 gradient를 받지 못합니다.
>
> 따라서 VQ-VAE에서는 임베딩을 학습시키기 위해 별도의 VQ 손실 항을 추가로 정의하고, 이를 통해 $e_i$를 업데이트합니다.
㉰ 따라서 임베딩 벡터들을 학습시키기 위해, 우리는 가장 단순한 dictionary learning 알고리즘인 벡터 양자화(Vector Quantization, VQ)를 사용한다. VQ 손실은 $\ell_2$ 오차를 이용하여 임베딩 벡터 $e_i$ 를 인코더 출력 $z_e(x)$ 방향으로 이동시킨다. 이 두 번째 항은 오직 코드북만 학습시키는 용도로 사용되며, 대신 moving average를 이용한 대체 업데이트 방식도 존재하지만, 본 논문에서는 사용되지 않았다.
㉱ 마지막으로, 임베딩 공간은 차원 단위가 없기 때문에, 만약 임베딩 벡터가 인코더보다 느리게 학습된다면 그 크기가 무한히 커질 수 있다. 이를 방지하고 특정 임베딩에 확실히 commit 하도록 유도하기 위해, 우리는 세 번째 항인 커밋 손실(commitment loss)를 추가한다. 이로써 전체 학습 목적 함수는 다음과 같이 정의된다.
$$
\mathcal{L} = \log p(x|z_q(x)) + \| \text{sg}[z_e(x)] - e \|_2^2 + \beta \| z_e(x) - \text{sg}[e] \|_2^2 \tag{3}
$$
여기서 $\text{sg}$는 stop-gradient 연산자로, 순전파 시에는 항등 함수처럼 동작하지만, 역전파 시에는 gradient를 차단하여 해당 항이 업데이트되지 않도록 고정한다. 디코더는 첫 번째 재구성 손실 항만을 최적화하고, 인코더는 첫 번째 항과 세 번째 커밋 손실 항을 최적화하며, 임베딩은 두 번째 VQ 손실 항만을 최적화한다.
[질문]
손실 함수는 입력과 출력의 차이 + 인코더 출력과 임베딩 벡터의 차이로 구성되어 있고,
여기에 임베딩 학습 속도가 인코더보다 느릴 경우 임베딩 벡터가 무한히 커지는 것을 막기 위해
추가 항(제약 손실, commitment loss)을 넣었다는 말인가요?
[답]
네, 정확히 맞습니다.
VQ-VAE의 전체 손실 함수는 다음과 같이 세 가지 항으로 구성됩니다:
$$
\mathcal{L} = \underbrace{\log p(x | z_q(x))}_{\text{재구성 손실}} +
\underbrace{\| \text{sg}[z_e(x)] - e \|_2^2}_{\text{VQ 손실 (embedding 학습용)}} +
\underbrace{\beta \| z_e(x) - \text{sg}[e] \|_2^2}_{\text{커밋 손실 (commitment loss)}}
$$
각 항의 의미
1. 재구성 손실
입력 $x$를 복원하는 능력을 최대화하는 항
→ 디코더와 인코더 학습에 관여
2. VQ 손실 (embedding 손실)
$z_e(x)$에 가까워지도록 임베딩 $e$를 학습시키는 항
(단, gradient는 stop-gradient 연산자에 의해 오직 $e$에만 적용됨)
3. 커밋 손실 (commitment loss)
임베딩이 인코더보다 느리게 학습될 경우, 인코더 출력 $z_e(x)$가
무한히 커질 위험이 있기 때문에, 인코더가 특정 임베딩에 "책임지고" 가까이 있도록
제약을 가하는 항
→ gradient는 $z_e(x)$에만 전달되고 $e$는 stop-gradient 처리됨
※ 커밋 손실 (commitment loss)
VQ-VAE에서 커밋 손실(commitment loss)은 인코더 출력 $z_e(x)$가 선택된 임베딩 벡터 $e_k$에 일정 수준 이상으로 가까이 머물도록 유도하는 제약 항이다. 이를 보다 직관적으로 설명하기 위해, 인코더 출력은 움직일 수 있는 물컵, 임베딩 벡터는 고정되거나 느리게 움직이는 자석에 비유할 수 있다. 이 비유에서 자석은 느리게 움직이는 특성을 가진 임베딩 벡터이고, 물컵은 학습 속도가 빠른 인코더의 출력이다. 인코더는 재구성 손실을 최소화하기 위해 자신이 생각하는 최적의 위치로 출력값을 계속 이동시키려 한다. 그러나 임베딩 벡터가 빠르게 적응하지 못하는 경우, 인코더 출력이 임베딩 벡터와 점점 멀어지는 방향으로 이동할 위험이 생긴다. 이 경우 양자화 과정에서 사용되는 임베딩 벡터는 실제 인코더 출력과의 의미 있는 연관을 점차 잃게 되고, 이는 모델의 표현력 저하나 학습 불안정성으로 이어질 수 있다. 이러한 문제를 방지하기 위해, 커밋 손실 항은 마치 자석 근처에 물컵을 잡아두는 탄성줄처럼 작동한다. 즉, 인코더 출력이 자신이 선택한 임베딩 벡터 근처에 일정 거리 이내로 머무르도록 강제하는 것이다. 수학적으로는 다음과 같은 항으로 표현된다:
$$\beta \| z_e(x) - \text{sg}[e_k] \|^2$$
여기서 stop-gradient 연산자인 $\text{sg}$는 이 항이 오직 인코더 출력 $z_e(x)$만을 업데이트하도록 제한한다. 따라서 이 손실은 인코더가 무한정 멀리 벡터 공간을 벗어나지 않도록 잡아주는 역할을 하며, 전체 모델이 보다 안정적으로 수렴할 수 있도록 돕는다. 결론적으로, 커밋 손실은 인코더가 선택한 임베딩에 대해 일정 수준의 “책임(commitment)”을 갖도록 유도함으로써, 양자화 표현의 일관성과 모델의 훈련 안정성을 보장하는 핵심 메커니즘이다.
요약 문장
> 임베딩이 인코더보다 느리게 학습되면 인코더 출력 $z_e(x)$가 무한히 멀어지려는 경향이 생기므로,
> 이를 방지하고 인코더가 특정 임베딩 벡터에 commit하도록 유도하는 제약 손실(커밋 손실)을 추가한 것입니다.
> 즉, 전체 손실은 재구성 정확도 + 임베딩 업데이트 + 인코더 출력의 안정성을 모두 조화롭게 고려한 구조입니다.
실험적으로 우리는 이 알고리즘이 $\beta$ 값에 대해 비교적 강건(robust)하다는 것을 발견하였고, $\beta = 0.1 \sim 2.0$의 범위에서도 결과 차이는 크지 않았다. 모든 실험에서는 $\beta = 0.25$를 사용하였으며, 일반적으로 이 값은 재구성 손실의 스케일에 따라 달라질 수 있다.또한, 본 논문에서는 $z$에 대해 균일 분포(uniform prior)를 가정하고 있기 때문에, VAE에서 ELBO에 등장하는 KL 항은 상수가 되며, 학습 시에는 무시될 수 있다.
실험에서는 $N$개의 이산 잠재 변수들을 정의하였으며, 예를 들어 ImageNet에서는 $32 \times 32$ 잠재 벡터 필드, CIFAR-10에서는 $8 \times 8 \times 10$ 구조를 사용한다. 결과적으로 얻어지는 손실 함수 $L$의 형태는 동일하지만, 각 잠재 변수(latent)마다 하나씩 존재하는 k-means 손실과 커밋 손실에 대해 총 $N$개의 항을 평균낸 것이라는 점만 다르다.
전체 모델의 로그 가능도 $\log p(x)$는 다음과 같이 근사적으로 계산할 수 있다:
$$
\log p(x) = \log \sum_k p(x|z_k)p(z_k)
$$
[질문]
생성 확률은 "입력 → 잠재변수 → 출력"의 흐름인데, 그렇다면 $p(x) = \sum_z p(x|z)p(z)$ 대신 입력 기반의 $p(z|x)$도 있어야 하는 것 아닌가요?
[답]
좋은 질문입니다. 하지만 생성 확률 $p(x)$를 계산할 때에는 입력 기반의 $p(z|x)$가 직접적으로 필요하지 않습니다. 그 이유는 생성 모델과 추론 모델의 방향이 다르기 때문입니다.
[질문]
그럼 생성 모델과 추론 모델의 차이가 정확히 무엇인가요?
[답]
생성 모델 (Generative model): 잠재변수 $z \sim p(z)$를 먼저 샘플링하고, $x \sim p(x|z)$를 생성합니다. 이때 전체 $x$의 확률은 다음과 같이 정의됩니다:
$$p(x) = \sum_z p(x|z)p(z)$$
추론 모델 (Inference model): 입력 $x$가 주어졌을 때, 이에 대응하는 잠재변수 $z$를 추정하는 분포 $p(z|x)$ 또는 근사 분포 $q(z|x)$를 사용합니다.
[질문]
그럼 학습에서는 $p(z|x)$를 전혀 사용하지 않나요?
[답]
이론적으로는 $p(z|x)$가 필요하지만, 실제로는 이를 계산하기가 매우 어렵기 때문에 근사 추론 분포 $q(z|x)$를 사용합니다. 이를 통해 변분 추론을 수행하며, ELBO(Evidence Lower Bound)를 최대화하는 방식으로 학습합니다:
$$
\log p(x) \geq \mathbb{E}_{q(z|x)}[\log p(x|z)] - D_{\mathrm{KL}}(q(z|x) \| p(z))
$$
[요약]
> 생성 확률 $p(x) = \sum_z p(x|z)p(z)$는
> 모델이 정의한 top-down 생성 과정에서 유도되는 수식이며,
> $p(z|x)$ 없이도 수학적으로 정확히 성립합니다.
>
> 다만, 학습 시에는 잠재변수 $z$에 대한 추론이 필요하기 때문에
> $p(z|x)$ 대신 근사 분포 $q(z|x)$를 사용하며,
> 그 결과 ELBO를 최대화하는 방식으로 모델을 최적화하게 됩니다.
하지만 디코더 $p(x|z)$는 학습 과정에서 항상 MAP 기반의 $z = z_q(x)$로부터 훈련되므로, 학습이 충분히 수렴한 경우 $z \neq z_q(x)$에 대해서는 거의 확률 질량이 할당되지 않느다. 따라서 근사적으로 다음과 같이 쓸 수 있다:
$$
\log p(x) \approx \log (p(x|z_q(x)) \cdot p(z_q(x)))
$$
이는 실험 4장에서 실증적으로 평가되며, Jensen 부등식(Jensen's Inequality)을 이용해 다음과 같이 하한으로도 쓸 수 있다:
$$
\log p(x) \geq \log (p(x|z_q(x)) \cdot p(z_q(x)))
$$
[질문]
식
$$
\log p(x) \geq \log \left( p(x \mid z_q(x)) \cdot p(z_q(x)) \right)
$$
는 왜 성립하나요?
이건 ELBO로 근사했을 때 KL divergence가 0보다 크기 때문인가요?
[답]
네, 맞습니다.
이 부등식은 변분 추론의 기본 원리에서 나오는 것이며, 핵심은 KL divergence가 항상 0 이상이라는 사실에 기반합니다.
더 구체적으로 설명하면 ELBO는 다음과 같이 정의됩니다:
$$
\log p(x) = \mathcal{L}(x) + D_{\mathrm{KL}}(q(z|x) \| p(z|x))
$$
여기서
$\mathcal{L}(x)$ = ELBO
$D_{\mathrm{KL}} \geq 0$
→ 따라서 항상 다음이 성립합니다:
$$
\log p(x) \geq \mathcal{L}(x)
$$
그리고 이 문맥에서의
$$
\log p(x) \geq \log \left( p(x \mid z_q(x)) \cdot p(z_q(x)) \right)
$$
는 사실 ELBO보다 더 단순한 근사로, MAP (Maximum a Posteriori) 추론을 이용한 근사입니다. 이 경우에는 $q(z|x)$ 대신 하나의 결정론적 선택 $z_q(x)$만 고려하므로
$\sum_z p(x|z)p(z)$ 대신 $p(x|z_q(x))p(z_q(x))$ 하나만 평가하게 됩니다.
당연히 이 경우에도 전체 합(혹은 적분에서 하나의 항만 뽑은 것이므로, 다음이 성립합니다:
$$
\log \sum_z p(x|z)p(z) \geq \log p(x|z_q(x))p(z_q(x))
$$
즉, 이건 Jensen’s inequality에 의해서도 항상 성립합니다.
요약
> 네, $\log p(x) \geq \log p(x|z_q(x))p(z_q(x))$가 성립하는 이유는,
> 전체 log-likelihood가 단일 샘플(MAP 추정치)로 근사된 값보다 항상 크거나 같기 때문입니다.
>
> 이는 근본적으로 KL divergence가 0 이상이고,
> Jensen 부등식에 의해 파생된 구조로 이해할 수 있습니다.
3.3 prior
이산 잠재 변수 $z$에 대한 사전 분포 $p(z)$는 범주형 분포(categorical distribution)이며, 특징 맵(feature map) 내의 다른 $z$에 의존하게 만들어 자기회귀적(autoregressive)으로 구성할 수 있다. VQ-VAE를 학습하는 동안에는 이 사전 분포를 고정된 균등 분포(uniform distribution)로 유지한다. 학습이 완료된 이후에는, 이산 잠재 변수 $z$에 대해 자기회귀적 분포 $p(z)$를 적합시켜, 조상 샘플링(ancestral sampling)을 통해 $x$를 생성할 수 있도록 한다. 이미지 생성에는 이산 잠재 변수 위에 PixelCNN을, 원시 오디오(raw audio) 생성에는 WaveNet을 사용한다. 사전 분포와 VQ-VAE를 동시에(jointly) 학습시키는 방법은 결과를 더 향상시킬 수 있지만, 이는 향후 연구 과제로 남겨두었다.
[질문]
이 문단을 보면, 특징 맵(feature map) 상에 여러 잠재 변수 $z$가 존재하고, 이 $z$들은 서로 완전히 독립은 아니고, 마치 LSTM의 hidden state처럼 일종의 의존성을 가진다고 해석해도 될까요?
[답]
네, 아주 정확한 이해입니다. VQ-VAE에서 특징 맵(feature map) 위의 이산 잠재 변수 $z$들은 각 위치마다 개별적인 categorical 변수이지만, 이들을 자기회귀적(autoregressive) 방식으로 모델링한다는 것은 이 변수들이 서로 조건부 종속성(dependence)을 갖고 있음을 의미합니다.
구체적 설명
1. 학습 중에는 사전 분포 $p(z)$는 고정된 균등 분포입니다. 즉, 학습 과정에서는 각 $z_i$가 독립적이라고 가정합니다.
2. 학습 후에는 실제로는 $z_i$들이 서로 의미적인 공간적/시간적 상관관계를 가지기 때문에, 이 구조를 더 잘 모델링하기 위해 자기회귀 모델을 사용합니다:
$$p(z) = \prod_{i} p(z_i \mid z_{<i})$$
여기서 $z_{<i}$는 $z_i$ 이전의 잠재 변수들을 의미하며, 즉 $z_i$는 과거의 잠재 변수에 조건부로 의존한다는 뜻입니다.
비유적으로 보면 이 구조는 LSTM의 hidden state처럼 고정된 순차적 상태는 아니지만, PixelCNN이나 WaveNet과 같은 자기회귀 구조에서, 각 $z_i$는 이전의 잠재 변수들에 따라 조건부로 결정되는 상태로 이해할 수 있습니다. 즉, 모든 $z_i$가 독립적인 범주형 변수가 아니라, 이전 $z$들과 통계적으로 연결되어 있다는 점에서 LSTM의 h 상태와 비슷한 해석이 가능합니다.
요약
> 네, 특징 맵 상의 잠재 변수들은 학습 중에는 독립으로 취급되지만,
> 학습 후에는 PixelCNN/WaveNet과 같은 자기회귀적 prior를 통해
> 서로 간의 조건부 의존성을 가지는 구조로 모델링됩니다.
>
> 이는 각 잠재 변수 $z_i$가 LSTM의 hidden state처럼
> 이전 정보에 기반한 예측 가능성을 갖는다는 점에서 비슷하게 이해할 수 있습니다.
4. Experiments
4.1 Comparison with continuous variables
본 실험에서는 CIFAR-10 데이터셋을 기반으로, VQ-VAE, 연속 잠재 변수를 사용하는 일반 VAE, 그리고 VIMCO를 동일한 아키텍처에서 비교하였다. 아키텍처는 두 개의 stride 2인 $4 \times 4$ 컨볼루션과 두 개의 residual 블록으로 구성된 인코더, 그리고 동일한 구조를 역순으로 갖는 디코더로 구성되며, 잠재 용량(연속/이산 변수 수, 이산 공간 크기 $K$)을 다양하게 설정하여 실험하였다. 최적화에는 ADAM(학습률 $2 \times 10^(-4)$)을 사용하고, 총 25만 스텝 동안 배치 크기 128로 학습하였다. VIMCO는 다중 샘플 학습 목표를 위해 50개의 샘플을 활용하였다. 실험 결과, VAE는 4.51 bits/dim, VQ-VAE는 4.67 bits/dim, VIMCO는 5.14 bits/dim의 성능을 보였으며, 이 값들은 모두 로그 우도의 하한(likelyhood lower bound)이다. 이 중 VQ-VAE는 이산 잠재 변수를 사용하는 모델 중 처음으로 연속 VAE 성능에 도전한 모델로, 상징적 표현(symbolic representation) 기반의 압축된 표현을 제공하면서도 일반 VAE와 유사한 재구성 품질을 달성하였다. 향후 절에서는 이 모델의 특징과 응용 사례를 소개한다.
※ 네트워크 구조
[입력: 32×32×3]
↓
[Conv1: 4×4, stride 2] → 16×16×256
↓
[Conv2: 4×4, stride 2] → 8×8×256
↓
[Residual Block #1]
- ReLU
- 3×3 Conv (256채널, 패딩 유지)
- ReLU
- 1×1 Conv (256채널)
- 입력과 출력을 덧셈(skip connection)
↓
[Residual Block #2]
- ReLU
- 3×3 Conv (256채널, 패딩 유지)
- ReLU
- 1×1 Conv (256채널)
- 입력과 출력을 덧셈(skip connection)
↓
[잠재 벡터/잠재 공간]
↓
[Residual Block #1]
- ReLU
- 3×3 Conv (256채널, 패딩 유지)
- ReLU
- 1×1 Conv (256채널)
- 입력과 출력을 덧셈(skip connection)
↓
[Residual Block #2]
- ReLU
- 3×3 Conv (256채널, 패딩 유지)
- ReLU
- 1×1 Conv (256채널)
- 입력과 출력을 덧셈(skip connection)
↓
[Transposed Conv1: 4×4, stride 2] → 16×16×256
↓
[Transposed Conv2: 4×4, stride 2] → 32×32×3
↓
[출력 이미지]
4.2 Images
본 실험에서는 128×128×3 이미지를 32×32×1 크기의 이산 잠재 공간으로 압축하고, 디컨볼루션 기반의 디코더와 PixelCNN 사전 분포를 결합하여 약 42.6배의 압축 효과를 달성하였다. 이를 통해 학습과 샘플링 속도를 크게 향상시키고, 이미지의 저수준 정보가 아닌 전역 구조를 효과적으로 모델링할 수 있음을 보였다.

※ 부연 설명
* 압축된 이산 잠재 표현 $z$의 크기:
$32 \times 32$ = 총 1,024개의 위치 (픽셀 격자처럼 생각)
* 각 위치마다 저장되는 값은?
코드북에서 하나를 선택해야 하므로, $K = 512$개의 코드 중 하나를 골라야 한다.
몇 비트가 필요한가?
* 512개의 선택지 → 몇 비트? 원=핫 벡터는 512차원 전체를 저장할 필요가 없고, 선택된 인덱스 k만 저장하면 된다.
$$\log_2(512) = 9 \text{비트}$$
즉, 각 위치에서 9비트짜리 이산 코드 하나를 저장하게 된다.
총 비트 수 계산
* 위치 수: $32 \times 32 = 1,024$
* 위치당 9비트 필요
→ 전체 비트 수:
$$
1,024 \times 9 = 9,216 \text{비트}
$$
※ 인코더–PixelCNN 연계 구조의 수식 기반 설명
1. 인코더: 이미지 → 이산 잠재 변수 $z$
원본 이미지 $x \in \mathbb{R}^{128 \times 128 \times 3}$는
인코더 $E(\cdot)$를 통해 이산 잠재 표현 $z \in \{1, ..., K\}^{32 \times 32}$로 압축된다:
$$
z = E(x)
$$
각 $z_{i,j} \in \{1, ..., K\}$: 코드북 $e \in \mathbb{R}^{K \times D}$에서 선택된 인덱스 보통 $K = 512$, 즉 9비트로 표현 가능
2. PixelCNN: $z$의 확률 분포 모델링
PixelCNN은 잠재 변수 $z$를 자기회귀(autoregressive) 방식으로 모델링합니다:
$$
p(z) = \prod_{i=1}^{32} \prod_{j=1}^{32} p(z_{i,j} \mid z_{<i,<j})
$$
여기서 $z_{<i,<j}$는 $(i,j)$보다 앞선 위치(예: raster scan 순서)의 모든 $z$ 값을 의미합니다. 이 모델은 다음을 학습합니다:
각 위치 $(i,j)$의 코드 인덱스 $z_{i,j}$가 이전 위치들에 조건부로 어떻게 결정되는지를 확률적으로 추정
이 구조를 통해 잠재 공간의 전역 패턴을 학습할 수 있음
3. 디코더: $z$ → 이미지 복원
압축된 $z$는 디코더 $D(\cdot)$를 통해 원래 이미지 $\hat{x}$로 복원됩니다:
$$
\hat{x} = D(z)
$$
디코더는 보통 deconvolutional network로 구성되어 있음
4. 샘플링 과정
학습이 완료되면, PixelCNN으로부터 $z \sim p(z)$를 샘플링하고, 이를 디코더에 넣어 새로운 이미지를 생성할 수 있습니다:
$$
x_{\text{sample}} = D(z), \quad \text{where } z \sim p(z)
$$
이산 잠재 공간(32×32×1)으로부터 복원된 이미지는 차원 축소에도 불구하고 원본과 거의 유사하며, 약간의 블러만 존재한다. 픽셀 기반 MSE 대신 GAN 기반의 인지 손실 함수도 가능하지만 이는 추후 연구 과제로 남겨두었다. 이후 단일 채널(흑백) 잠재 공간에 대해 PixelCNN 사전 분포를 학습하였으며, 색상 대신 공간 마스킹만 적용하였다. 사용된 PixelCNN의 용량은 기존 논문 수준과 유사하다. PixelCNN에서 샘플링한 결과는 VQ-VAE의 디코더를 통해 픽셀 공간으로 변환되었으며, 그림 3에 제시되어 있다.
※ 전체 과정 요약
1. PixelCNN 사전 분포 학습
* ImageNet 이미지들을 인코더에 넣고 → 이산 잠재 표현 $z \in \{1, ..., K\}^{32 \times 32}$ (K=512)를 추출
* 이 $z$들을 학습 데이터로 하여 PixelCNN이 $p(z)$를 학습
* 즉, 이산 잠재 공간에서의 조건부 분포 $p(z_{i,j} \mid z_{<i,<j})$를 모델링
2. 샘플링
* 학습된 PixelCNN으로부터 새로운 $z$ 샘플을 자기회귀적으로 생성
* 이 $z$는 32×32 격자의 이산 인덱스들로 구성된 벡터 행렬임
$$
z = \begin{bmatrix}
z_{1,1} & z_{1,2} & \dots & z_{1,32} \\
z_{2,1} & \dots & \dots & z_{2,32} \\
\vdots & \vdots & \ddots & \vdots \\
z_{32,1} & \dots & \dots & z_{32,32}
\end{bmatrix}, \quad z_{i,j} \in \{1, ..., 512\}
$$
* 각 $z_{i,j}$는 코드북 $e_k \in \mathbb{R}^D$에서 선택할 수 있는 인덱스이며, 최종적으로 이산 인덱스를 벡터로 매핑하여 사용할 수 있음
3. 복원
* 위에서 샘플링한 $z$를 VQ-VAE 디코더에 넣고,
* 각 인덱스 $z_{i,j}$에 대응되는 임베딩 벡터 $e_{z_{i,j}} \in \mathbb{R}^D$를 찾아 구성한 $z_q(x) \in \mathbb{R}^{32 \times 32 \times D}$를 디코더 입력으로 사용
* 디코더는 이 $z_q(x)$로부터 128×128 RGB 이미지를 복원

다음 실험에서는 DeepMind Lab의 84×84×3 프레임에 대해 VQ-VAE를 적용하였으며, 21×21×1 잠재 공간으로 압축한 후에도 복원 이미지가 원본과 거의 동일한 품질을 보였다(Figure 4 참조). 이후 이 잠재 공간 위에 PixelCNN을 학습하고, 디컨볼루션 디코더를 통해 샘플을 복원하였다. 추가로, 해당 잠재 공간을 입력으로 하는 두 번째 VQ-VAE를 구성하고 PixelCNN 디코더를 탑재했음에도 posterior collapse 없이 잠재 변수가 의미 있게 활용되었다. 두 번째 VQ-VAE에서는 총 3개의 이산 잠재 변수만 사용하여 float32보다 적은 용량(3×9비트)으로 이미지를 압축하고 복원했으며, 결과는 Figure 5에 시각화되어 있다.


4.3 Audio
이 실험에서는 원시 오디오 데이터에 대한 이산 잠재 변수(discrete latent variables)가 어떻게 작동하는지를 평가하였다. 이를 위해 WaveNet 디코더와 유사한 팽창 합성곱(dilated convolutional) 구조를 갖는 VQ-VAE를 사용하였으며, VCTK 데이터셋(109명의 화자 포함)을 대상으로 실험을 수행하였다. 인코더는 스트라이드 2, 커널 사이즈 4를 갖는 합성곱층 6개로 구성되어 있어, 원본 waveform보다 64배 압축된 이산 잠재 표현을 생성한다. 이 잠재 표현은 하나의 feature map으로 구성되며, 이산 공간의 크기는 512이다. 디코더는 이 잠재 표현과 화자 정보를 담은 원-핫 임베딩을 입력으로 조건부 샘플링을 수행한다. 실험 결과, 디코더로 복원한 음성은 텍스트 내용은 동일하지만 waveform의 형태와 억양은 다소 달랐으며, 이는 VQ-VAE가 언어적 감독 없이도 저수준 특성에는 불변하고 고수준 의미(예: 문장 내용)만을 보존하는 추상화된 잠재 표현 공간을 학습했음을 시사했다. 이 결과는 중요한 특징들이 종종 원본 데이터 공간에서 여러 차원에 걸쳐 존재한다는 기존의 관찰을 뒷받침한다. 이 실험에서는 원시 오디오로부터 추출한 이산 잠재 표현 위에 사전 분포를 학습하여, 장기적인 의존성을 모델링하였다. 460명의 화자 데이터를 사용하고, 해상도를 128배 축소한 VQ-VAE를 통해 2.56초 길이의 오디오 조각을 320개의 잠재 timestep으로 압축하였다. 기존 WaveNet은 웅얼거림 같은 출력을 보였지만, VQ-VAE는 명확한 단어와 문장 일부를 생성함으로써, 비지도 방식으로 음소 수준의 언어 모델을 학습할 수 있음을 입증하였다. 다음으로 한 화자의 음성을 인코딩한 잠재 표현을 다른 화자의 ID로 디코딩하여 화자 변환을 수행하였다. 결과적으로 음성의 내용은 동일하지만 목소리만 다른 화자로 재생성되었으며, 이는 VQ-VAE가 화자 고유 정보와 음성 내용 정보를 성공적으로 분리하여 잠재 공간에 표현했음을 보여준다. 예를 들어 설명하자면, VQ-VAE가 만들어낸 128차원의 이산 코드 공간을 초당 25개(샘플당 40ms)로 출력하도록 한 뒤, 이 128가지 코드 각각을 41가지 실제 음소(phoneme) 중 하나에 "가장 가능성 높은 음소"로 대응시키는 매핑을 미리 만들어 두었다. 그런 다음 실제 음성 데이터를 인코더에 넣어 생성된 코드들을 이 매핑대로 음소 시퀀스로 변환했더니, 41개 클래스 분류 정확도가 49.3%에 달했다. 참고로, 무작위로 배정된 코드 공간에서는 전체 음소 중 가장 빈도가 높은 하나만 예측해도 약 7.2%의 정확도 밖에 얻지 못한다. 이 결과는 전혀 지도학습 없이 얻은 이산 잠재 코드들이 음성의 고차원적인 특징, 즉 음소 구조와 밀접하게 대응한다는 강력한 증거라고 볼 수 있다.
4.4 Video
DeepMind Lab 환경에서 VQ-VAE를 이용해, 행동 시퀀스를 조건으로 잠재 공간 $z_t$만으로 16프레임짜리 비디오를 생성했다. 실제 픽셀 대신 이 잠재 벡터를 결정적 디코더로 매핑해 이미지 품질 저하 없이 부드럽게 시퀀스를 이어붙였으며, 행동을 주지 않은 경우에도 유사한 결과를 얻었다.

5. Conclusion
VQ-VAE는 벡터 양자화를 통해 이산 잠재공간을 도입한 새로운 VAE 계열로, 128×128 컬러 이미지 생성과 행동 조건 비디오 합성, 비지도 음성 생성 및 화자 변환 등에서 장기 의존성을 효과적으로 모델링하고, CIFAR-10 데이터셋에서는 연속 잠재변수 모델과 거의 동등한 성능을 보이며, 완전 비지도 학습만으로 음소 수준의 언어 표현까지 습득했다는 점에서 주목할 만하다.